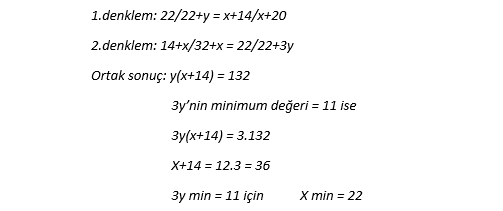‘Altın koridorlar’
Açılış
İlk yazıda futbol kurallarının sahaya geometrik yansımalarından bahsetmiştim. Bu kez “sahanın başka bir şekilde görülüp görülemeyeceğinden” bahsedeceğim. Futbol sahasına başka bir şekilde bakarsak, oyuna dair yeni sonuçlara ulaşabilir miyiz? Futbol tarihindeki ve fakat özellikle son dönemdeki akımlar bu şekilde izah edilebilir mi?
Yazı dizisinin devamında sırasıyla bu sorulara yanıt ararken bu yazıda futbol sahasının altın oran ile ilişkisini, Fibonacci’nin sayı dizisi ve geometrik yansıması olan altın dikdörtgenlerin futbol sahasının bir başka görünümüne imkan tanıyışını değerlendireceğim. Futbol sahası, alıştığımızdan farklı biçimde görülebilir mi?
Ama öncelikle futbol sahası ve “Fibonacci sayı dizisi” ile “altın oran ve türevleri” arasındaki ilişkiyi nasıl kurduğumu açıklamak için ceza sahası ölçüleri ve sahanın boyutlarına dair bir şeyler anlatmalıyım.
Sabitler ve değişkenler
Futbol sahasının ölçüleriyle ilgili dikkat çekici bir konu var. Dünyanın her yerindeki resmi futbol sahalarında asla değiştirilemeyecek sabit ölçüler olmasına rağmen sahanın boyu ve eninin kati bir değeri yok. Bu nedenle farklı statlardaki sahaların eni ya da boyu farklılık gösterebiliyor. Son zamanlardaki standardizasyon çalışmaları ve uluslararası maçlardaki daha dar ölçü aralığına rağmen bu durum, başka bir soruyu akla getiriyor. Sahayı ilk kez çizen, istese tüm ölçüleri sabit hale getiremez miydi?
Oysa o, çemberler arasındaki mesafeyi sabitlememiştir; bu yüzden saha ölçüleri belirli sınırlar dahilinde kalmak şartıyla değişebilmektedir. Gerekçe yüksek ihtimalle her yerde aynı genişlikte oyun alanlarının bulunamayacak olmasıydı. Fakat imkanı olsa, tüm bu hesaplamalar ve geometrik araçlar vasıtasıyla sahayı kuran kişi, sahanın değişmez-sabit boyutlarda olmasını istemez miydi?
O zaman mesele, “o boyutların ne olacağına” geliyor. Bunun için de konuya ilk yazıda kaldığımız yerden, ceza sahasının oluşumundan başlamamız gerek.
Kaldığımız yerden
İlk yazıda kale sahasını geometrik araçlar vasıtasıyla gerçek ölçüleriyle oluşturarak sahanın yapısını izah etmiştim. Devamında bir “fark alanı” eklenerek oluşturulacak “ceza sahası”ndan ve sahanın altın orana göre önem arz eden bazı alanlarının bu fark alanıyla ilişkisini anlatacağımı söylemiştim.
Öyleyse ceza sahasının geometrik izahı ve ardındaki düşünceden başlayabiliriz:
“Ceza sahası” neden var ve niye orada?
Açıkça söylemek gerekirse ceza sahasının varlığı ve boyutları, futbolda altın oranı incelemeye başladığımdan beri sebebini tam olarak çözemediğim bir konuydu. İlk yazıda bahsettiğim saha şekillerinin ve ölçülerinin ispatında faydalandığım geometrik araçlar ceza sahasının oluşumu için geçerli değildi. İlk yazıdaki dış açıortay ya da uzantısı üçgenler vasıtasıyla çıkan alan, gerçek sahadaki “ceza sahası” ölçüleri ile örtüşmüyordu.
Hal böyle olunca sahaya başka bir açıdan daha bakmak gerektiğini fark ettim. Çözümler, yeni bakış açıları gerektirir. Bu yüzden sahanın dünyanın hiçbir yerinde değiştirilemeyecek “sabit ölçülerinden” hareket ettiğimde elimde 22 yard’lık değişmez bir uzunluk olduğunu fark ettim.
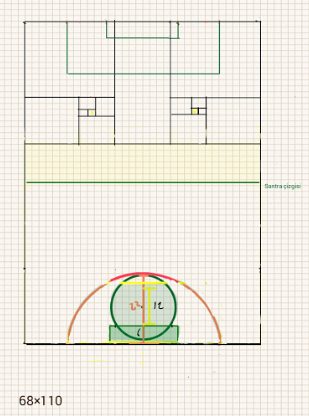
Yeşil dikdörtgen, kale sahasını temsil ediyor. Kaleden çıkan turuncu doğrunun uzunluğu 22 yard.
İlk yazıda hikayesini anlattığım “silinen çemberler”den 2 yard uzaklıkta konumlandırılmış kaleden çemberin diğer ucuna; yani ceza yayına, değişmez bir 22 yard var. Dünyanın tüm futbol sahalarında, kalenin orta noktasından ceza yayının en uç noktasına uzaklık 22 yard olmak zorunda. Bu değişmez uzunluktan düşünmeye başlayınca “eş uzaklıklar fikri” ile yarıçapı 22 yard olacak yeni bir çember çizilse bunun nerelere uzanacağı üzerine düşündüm. Şöyle bir sonuç ortaya çıktı:
Yarıçapı 22 yard olan yeni çember.
Kalenin ortasından ceza yayına uzanan yarıçap gibi, aynı noktadan bu kez yatay eksende bir yarıçap çizildiğinde bu doğrunun ulaştığı nokta, kale sınırından 18 yard uzaklıkta. Kalenin iki yanından 18 yard uzaklıkta ceza sahası böylece ortaya çıkıyor. Kaldı ki burada tıpkı silinen çemberlerin hikayesinde anlattığım gibi 6 yard ve 12 yard’lık uzaklıklarla oluşan “2ye1” ve “3e2” gibi benzerlikler meydana geliyor. Ki bu oranlar, biraz ilerisi için önemli.
Kaleden 18 yard uzaklıktaki nokta, kale sahasından 12 yard uzakta kalıyor.
Birazdan açıklayacağım adalet ve eşitlik nosyonu gereği ceza sahasının dikey uzunluğunun da 18 yard olması gerekiyordu. Bu nedenle ilk yazıda bahsettiğim gibi dikdörtgenler içinde kalan çember silinirken 4 yard dikey uzunluğundaki bir yayı, varlığını koruyabiliyor.
Ceza sahası ortaya çıkıyor.
Ceza sahasının ölçülerini matematiksel olarak açıkladığımıza göre, “ardındaki düşünce”ye geçebiliriz:
Eşitlik, kalecilik ve adalet
Futbolda sahanın bütün çizimini dayandırdığım “duran oyunda rakibin en az 10 yard uzak olması gerekliliği”ne dair ihtiyatlı yaklaşım, penaltı anındaki kaleci için ise istisnai bir duruma sahip. Durumun kendisi istisna teşkil etmiyorsa da kaleciler açısından daha ağır şartlarda düzenlenmiş bir kural var. Penaltı noktasına top konduğunda kaleci çizgi üstünde hareket etme özgürlüğüne sahiptir; ancak ileri çıkamaz. Bu da kalecinin penaltı anında topa 12 yard uzaklıkta olması demek. Burada “duran oyunda rakibin konumu” kuralında 10 yard’lık mesafeye daha sıkı bir şekil şartı getirilmiş oluyor. Tam da bu noktada eşitlik gereği “kaleci, duran oyunu başlatırken” rakibin konumu gündeme geliyor.
Ceza sahasının varlığının “sebebi” duran oyundaki bu mesafe eşitliği fikri. “Nasıl”ını ise, geometrideki eşit mesafeler timsali çemberler gösteriyor.
Bildiğiniz üzere kale vuruşları, kural olarak, kale sahası (six yard box-altıpas) çizgileri üzerinden kullanılır. Son zamanlarda basketboldaki gibi tam saha baskının olağanlaştığı günümüz futbolunda, kaleci kale vuruşunu kullanırken kimse “ceza sahasına” giremez. Kendi arkadaşları dahil tüm oyuncular en fazla ceza sahasının hemen dışında oyunun harketlendirilmesini bekleyebilir. Ceza sahası dışındaki bu bekleme alanları, kalecinin oyunu başlatacağı noktadan “en az 12 yard” uzaklıktadır.
Bir kez daha futbolun matematiği ve mantığı, birbirini sağlıyor. Koyu yeşil renkle gösterilen kale sahasından kale vuruşu kullanılırken, “sarı çizgiyle temsil edilen ceza sahası sınırları” vuruşun kullanılacağı herhangi bir noktadan az 12 yard uzak.
Yukarıda matematiksel olarak gösterdiğim 18 yard’lık ceza sahasının kale sahasından kalan 12 yard’lık kısmı bu eşitlik ve adaleti sağlamış oluyor. Bu nedenle yarıçapı 22 yard olan çemberin dikey kolu da 18 yard’lık noktada kesilip buradan ceza sahasının sınırları oluşturuluyor. Böylece duran oyunda kaleci, kale vuruşuyla oyunu başlatacakken herkes “en az” 12 yard uzakta.
Sahanın “değişebilen” boyutlarına gelirsek
Ceza sahasının ölçülerini açıkladıktan sonra artık sahanın ilk halindeki üç çemberin arasında kalan mesafenin değişkenliği ve başlarken belirttiğim “olması gerekenin” ne olduğu meselesini tartışabiliriz. Ki bu mesele, bizi altın orana götürecek…
Futbol sahasının ilk hali
Artık elimizde kaleden 22 yard sabit uzaklıkta olduğunu bildiğimiz bir ceza yayı, 18 yard olduğu kesinlik kazanan ceza sahası ve böylece yatay eksende, dünyanın hiçbir sahasında değişmez uzunluğu 44 yard olan bir “ceza sahası” var. Ceza sahasının ölçülerini ispat etmeden sahanın eni ve boyu hakkında konuşamazdık…
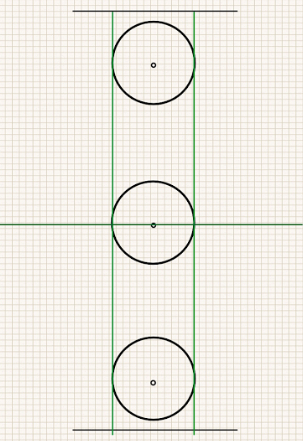
44 yard enindeki ceza sahası. Kalenin ortasından 22 yard’lık iki eş parçaya bölünüyor.
Çemberler arası mesafeyi (x) bularak ulaşacağımız sahanın boyuna geçmeden önce sahanın eni hakkında önemli bir şey söylemem gerekiyor.
Sahanın boyunda çemberler sebebiyle değişmez uzunluklar olduğu gibi, sahanın eninde ceza sahasının oluşturduğu 44 yard’lık bir sabit olduğunu belirtmiştim. Fakat sahanın eninde bir değişmez daha var. “En”in alabileceği asgari değeri bulabilmek için bu değişmezi de hesap etmeliyiz.
Köşe gönderinin etrafındaki çizgiler
Çokça üstünde durduğum gibi futbol sahası, oyunun durduğu anlar ve bu anlarda rakibin konumu üzerine inşa edilmiş gibi görünüyor. Bu noktada henüz konusu geçmemiş ama sahanın boyutlarının belirlenmesi için önemli bir meselenin daha açıklanması gerekiyor: köşe vuruşları.
Oyunun durduğu anlardan biri olan köşe vuruşları için sahada bir işaretleme var. Futbol sahasında duran topların kullanılacağı noktalar için (penaltı, santra, kale vuruşu, köşe vuruşu) tüm çizimler yapılmış. Serbest vuruş, endirekt vuruş gibi diğerleri ise maç esnasında sahanın her yerinde olabileceğinden bu durumlarda 10 yard uzaklığı hakemler ölçüp gösteriyor.
Çoğumuzun gözünden kaçmış ya da yedek futbolcuların ısınma sınırları için konduğunu sanabildiğimiz bir çizgi, aslında duran oyunda rakibin konumunu ayarlamak için oluşturulmuş. Sahaya dikkatle baktığınızda köşe noktalarının iki yanında 10 yard uzaklıkta birer çizgi olduğunu görüyoruz. Köşe vuruşu kullanılırken topun konduğu noktadan rakibin en az 10 yard uzaklığını sağlamak için kondurulmuş bu çizgiler topun konduğu 1 yard yarıçapındaki çeyrek çemberler de hesaba katıldığında “ceza sahasının bitiş noktasından sahanın sona erdiği köşe gönderine” en az 11 yard’lık bir mesafeyi zorunlu kılıyor. Bu da futbol sahasının yatayda en az 66 yard’lık bir uzunluğa ihtiyacı olması demek.
Bahsettiğim çizgiler aşağıda, mavi olanlar. Diğerleri altın dikdörtgen sınırları için.
Böylece futbol sahasının eninin alabileceği asgari uzunluğu belirledikten sonra tekrar sahanın “boyuna” dönebiliriz. Bizi kaleden santra noktasına çekilecek bir boy çizgisi karşılıyor. Köşe gönderine uzanacak bir çizgi daha çektiğimizde büyük bir üçgen oluşuyor:
Sahanın eninin en az 66 yard olması gerektiğini artık biliyoruz. Bu asgari yatay eksen uzunluğundan faydalanarak uzunluğu 33 yard olan kenara ulaşıyoruz. Bu kenardaki bilinmeyenimizin (görselde 3y) alabileceği en düşük değer 11 yard. Elimizde şöyle bir oran-orantı denklemi oluşuyor:
Üçgenlerde ve oran-orantı denklemlerinde kullanılan bu sayıların açıkça görünmesi gerekiyor. Çünkü görselde ve denklemlerde geçen 14,22,32,54 sayı doğrusunda Fibonacci dizisindeki sayılarla komşu.
X uzunluğunun asgari değeri 22 iken yarı saha uzunluğu (32+x) olduğundan yarı sahanın uzunluğu en az 54 yard olmalıdır. Bu ölçümlere göre asgari saha uzunluğu 108, en 66 yard’dır.
Bu asgari en-boy değerleri ve altın oran etrafındaki diğer saha ölçülerine göre sahanın altın alanları hesaplanabilir. Fibonacci sayılarına göre bir saha oluşturulursa bu sahanın ölçüleri de 110×68 yard oluyor. FIFA’nın belirlediği 105 metreye 68 metre standart ölçüsü de yaklaşık olarak 114×74 yard’a denk geliyor.
Asgari boyutlardaki saha
Sahanın Fibonacci sayıları ile çizilmiş boyutları ( Yarı uzunluklar: 34-55 yard )
Altın oran: estetik ve işlevsellik
12, 14, 22, 32, 54 … Saha boyutlarının alabileceği değerlerin gezindiği bu aralık Fibonacci sayı dizisinin eşiğine düşüyor. Fibonacci sayılarının her biri, kendisinden bir önceki sayıya bölündüğünde yaklaşık; bir noktadan sonra “aynı oranı” veriyor: altın oran.

Böylece sahanın başlangıçtan itibaren oluşumunu adım adım izlediğimizde, aslında Fibonacci’nin sayı dizisinin etrafında dolaştığımız ortaya çıkıyor.
Bu noktadan itibaren, bir çemberden başlayarak meydana gelişini açıkladığım futbol sahasının, başka bir açıdan bakıldığında farklı görülebileceğine dair savımı ispat etmek için sahaya, altın oran ve türevleri; altın dikdörtgen, altın alan ve altın merkez üzerinden yaklaşacağım. İlk yazıda futbol sahasının neden sadece yatay değil dikey de görülmesi gerektiğini açıklamaya çalıştığım gibi, şimdi de futbol sahasına “daha farklı ve değişken” bir şekil olarak yaklaşılabileceğini anlatacağım. Sahayı altın alanları ve diğer sınırlarıyla gördüğümüzde oyunu başka bir şekilde açıklayabiliriz. Başka bir gözle bakabileceğimiz için artık, baktığımız yerde yeni şeyler görebiliriz.
Öncelikle, kısaca “altın oran” nedir?
Futbol sahasındaki bu korelasyonun müsebbibi altın oran, günlük hayatta birçok alanda karşımıza çıkan matematiksel bir “estetik” formülasyonu. Mimari, görsel sanatlar, insan vücudu ile çevremizdeki gördüğümüz eşya arasında ortak bir oran var. İnsan beyni bu orana yaklaşan şeylerden hoşlanma ve etrafında bu oranı arama eğiliminde. Kağıt üzerine çizilecek bir futbol sahasında da. İki boyutlu kağıt üzerinde sahanın düzgün çizilmesi için faydanılmış altın oran, üzerinde top oynanan üç boyutlu bir sahaya döndüğünde estetik maksatlar, işlevsel alanlar yaratıyor.
Altın dikdörtgen nedir, altın alana nasıl ulaşılır?
https://giphy.com/gifs/xUOwGfvaushkXn4N7q
Fibonacci’nin sayı dizisi, her biri kendinden önceki ardışık iki sayının toplamıyla oluşan sayıların, bir önceki sayıya bölündüğünde yaklaşık olarak aynı, bir yerden sonra tamamiyle aynı oranı verdiği bir dizidir. Bu sayı dizisi, çemberler vasıtasıyla geometrik olarak ifade edildiğinde ortaya muntazam şekiller çıkarır. Bu şekiller altın nitelendirmesiyle anılır ve altın alanlara sahiptirler. İnsan beyninin aradığı oranları haiz olduklarından bu şekiller, göze hoş görünür ve estetik olarak muntazamdır.
İşte dikdörtgen şeklindeki futbol sahası, Fibonacci dizisindeki ardışık sayıları kısa ve uzun kenar olarak kendine aldığında, altın alanlara sahip bir altın dikdörtgen meydana gelir. Altın orana göre oluşturulmuş dikdörtgenler içerisinden kareler çıkarıldığı sürece kalan şekiller, kenar uzunlukları arasında altın oranı korumaya devam eder. Fibonacci’nin sayılarındaki bir sayı nasıl kendisinden önceki sayıların toplamına eşitse bu dizideki bir sayıdan kendisinden bir önceki sayıyı çıkardığımızda önceki sayıya ulaşmışız demektir.
https://giphy.com/gifs/l1KcPket8iyZWYzII
Bu matematiksel işlemi altın dikdörtgenden kareler çıkararak uyguladığımızda elimizde her seferinde yine altın orana sahip kenar uzunluklarını haiz dikdörtgenler kalır. Ta ki ilk Fibonacci sayısına ulaşana kadar. İşte bu son kare ve o son nokta, söz konusu şeklin altın merkezidir. Ondan önceki her seferinde elde kalan altın dikdörtgenler ise “bu altın merkeze yaklaştığı yoğunlukta” dikdörtgenin altın alanlarıdır.
Bu çıkarma işlemini sahanın dört farklı köşesinden yaparak sahadaki dört altın alanı ve altın dikdörtgen sınır çizgilerini bulabilirz. Böylece görmeye alışık olduğumuzdan farklı bir sahayla karşılaşırız.
https://giphy.com/gifs/l0NgSp7PKHaxv69Ow
Daha rahat görülebilmesi adına yarı saha uzunluğu olarak 55, enin yarı uzunluğu olarak 34 alacağım. (Hatırlanacağı üzere bu değerlerin alt sınırı sırasıyla 54 ve 33’tü.) Saha her birinin iki katından oluştuğundan görsellerdeki sahanın boyutları 110×68 yard’dır.
Şu ana kadar yazıdaki tüm saha görselleri en az bir altın alan ve türevi (sarı renkli alanlar ve mahalli) içeriyordu. Burada dört altın alan, ve bu alanları ortaya koymak için çıkarılan tüm altın dikdörtgenler görülebilir. (Görseldeki yeşil çizgiler sahada aşina olduğumuz alanları gösterirken siyah çizgiler altın dikdörtgenler vasıtayla çizilmiştir).
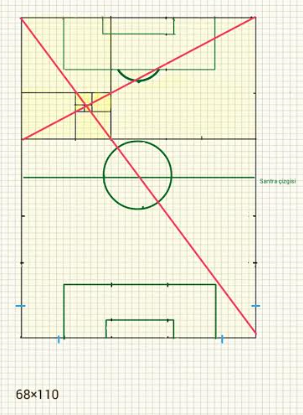
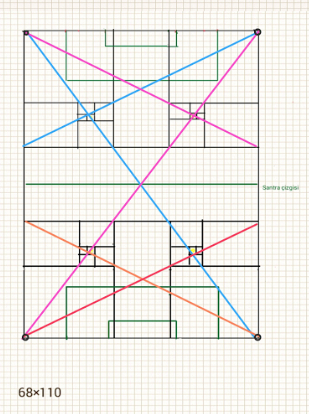
Altın merkezlerin birinden geçen köşegenler. Sarı renk yoğunluğu, altın merkeze uzaklığa göre altın alan vasfını temsil ediyor.
Bunlar da altın merkezlerin ve buralardan geçen köşegenlerin tümü. Mavi ve pembe renkteki büyük köşegenlerin kesiştiği yer, santra noktası. Aynı renkteki küçük köşegenlerin ve turuncu kırmızı küçük köşegenlerin kesiştiği noktalar ise ceza yayı.
Altın koridorlar
Nihayetinde iki yazıdır anlatmış olduğum “fark alanları” ve “altın alan mahalli” birleştirildiğinde sahada iki koridor meydana geliyor:
https://giphy.com/gifs/l0NgQzuT2W4S5uhpe
Sahanın boyutları büyüdükçe altın alan ve koridorlar açısından bölgesel olarak değişen bir şey olmuyor. Altın koridorlar “fark alanı” olarak adlandırdığım ceza sahasının bu bölgesinin içinden geçmeye devam ediyor.
Orijinal lafzıyla “half-space”, sahanın 4 altın alanı ve ceza sahasının “fark alanı”nın birleştirilip uzatılmasından oluşuyor. Bu koridorun tehditkarlığı, işlevselliğinden geliyor. Ve işlevselliği de iki boyutlu kağıt üzerindeki sahanın oluşumunda “estetik amaçlarla” kullanılan altın oranın; üzerinde futbolcuların oynadığı üç boyutlu futbol sahasına dönüştüğü anda hasıl oluyor. “Half-space” olarak anılan bu altın koridorlar, sahanın altın alanlarını barındırdığından öneme sahip. Ona kıymetini veren, altın alanlar üzerinde olması.
Altın alanların birbirlerine bağlandıkları bu koridorlar kadar kendi varlıkları da ayrıca bir öneme sahip. Zira bu alanların bizatihi kendileri hücumda son pasları vermek ve oyunu yönlendirmek için oldukça kıymetli. Bu bölgelerden çıkan paslar ve bu bölgeler merkeze anılarak yapılan toplu/topsuz oyunlar, rakip savunmanın dengesini bozuyor. Bu alanlardan çıkan paslar özellikle fark alanlarına yöneldiğinde pozisyonun golle neticelenme ihtimali artıyor.
Akış
Kağıt üzerindeki futbol sahasının en kıymetli noktası altın merkezleri. Nasıl ki bir fotoğrafta “obje” belirli bir noktaya denk getirildiğinde göz ilk onu fark ediyor ve bu obje göze “olabilecek en estetik” haliyle yansıyorsa, oyuncuların da bu altın merkez ve mahalindeki altın alanlarda bulunmasının ideal hücuma ve verimliliğe bir etkisi var.
Zira günümüz futbolunda çoğunlukla alan ve pozisyon oyunu oynanıyor. Bu da sahanın iyi kavranmasını ve farklı bakış açılarından yaklaşılarak oyuna dair yeni fikirler ve taktikler geliştirilmesini talep ediyor. Bu yüzden sahaya başka bir gözle bakmak, sahanın kullanımı ile oyuncuların bulunması ve yönelmesi gereken alanlar konusunda daha “etkili” çözümler bulunabilmesine olanak tanıyacaktır.
Tabii ki altın oranın futbol sahasındaki alameti, estetik değil. Çünkü futbol, anlık bir resim değil; hareketten ibaret bir akış. Ama tıpkı karelerden oluşan filmlerin her bir anındaki kareler gibi, futbolda da sahada bulunulacak alınacak pozisyonlar ve set oyunları, akış halindeki oyunun neticesini belirleyecektir. Mesele oyuncuların bu alanda bulunması ya da orada durmaları değil ortalama olarak bu alanlar ve mahallinde oyunu yönetip ve münferit pozisyonları oynamalarıdır. Zira futbol da filmler gibi nihayetinde pozisyonların birleşiminden ibaret.
https://giphy.com/gifs/l0NgQzuT2W4S5uhpe
Futbol sahasının çiziminin, oyunun belirli bölgelerden oynanmasını dikte ettiğine inanıyorum. Kağıt üzerindeki estetik, üzerinde top oynanan sahada işlevselliğe dönüşüyor. Altın oran, futbolu altın koridorlardan oynamaya teşvik ediyor. İşte sahaya başka bir yerden yaklaşıp onu başka şekillerde gören teknik adamların farkına vardığı, bu alanlar.
Bu alanları ve onları birbirine bağlayan koridorları kullanan takımlar bu yüzden başarılı oluyor. Gerek müdafaada gerekse hücumda bu alanları hesap ederek oyunlarını kurguladıklarından. Oyuncularını bu alanlarda konumlandıran, topu burada döndüren, pozisyona girecek koşulara bu bölgedeki duruma göre başlayan; bazen bilinçli olarak bu alanları boş bırakan, rakibi bu bölgelere yönlendirerek sıkıştıran, baskıyı bu bölgede yapan; hücumda iken savunmacılarının duracağı yeri bu sınırlar ve alanlara denk düşecek şekilde planlayan takımlar, oyunu kazanıyor.
Görünen o ki dahası da var… Elimizde değişmeyecek oyun kuralları ve üzerinde radikal değişimler olmayacak bir oyun sahası var. Fark yaratabilmek için oyuna ve sahaya bakış açımızı sürekli güncellememiz gerekiyor.
Kapanış: “Peki bunlar gerçek hayatta ne işimize yarayacak?”
Tıpkı altın oranın sahadaki yansımasını anlatmak için öncelikle sahanın ilk çizilişini ve ardındaki matematikle mantığı anlatmam gerektiği gibi, futbol sahasında oynanan oyunların altın orana denk düştüğünü göstermek için de altın oran ve türevlerinin futbol sahasıyla ilişkisini anlatmam gerekiyordu.
Üçüncü yazıda tüm bu bahsettiklerimin doğruluklarını göstermek için “altın alanlardan yapılan hücumlar ve organize edilen ataklar” ile “altın koridorların kullanımı”; “savunmada altın oran ve türevlerinin işlevi” ve “altın dikdörtgen sınırlarının hücum ve savunmadaki bazı aksiyonlarla rastlantısı” konusunda örnekler sunacağım.
Estetik, işleve hizmet edecektir. Neden ve nasıl? Bu iki yazıda, futbol sahasının çiziminin ardındaki geometri ve matematik üzerinden “nedenini” açıklamaya çalıştım. Son yazıda ise bunun “nasıl” mümkün olabileceğini göstermeye gayret edeceğim.
Sahayı ölçtük, biçtik; kesip çıkarıp başka alanlar inşa ettik. Fi ve geometri bitti. Sıra futbolda. Bir sır varsa o sahada çözülecek.